Вълновите функции не са достъпни за никакво експериментално определяне; те могат единствено априори да бъдат изчислени. Те се получават като решение на едно диференциално уравнение, наречено уравнение на Шрьодингер:

E: пълната енергия на електрона

V: потенциалната енергия на електрона

m: масата на електрона

h : константа на Планк 

Решенията на това уравнение трябва да отговарят на определен брой условия: функцията 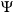 трябва да бъде единствена, крайна и непрекъсната по отношение на x, y и z ; тя трябва освен това да задоволява условието, изразено от уравнението по-горе.

В резултат на това уравнението на Шрьодингер има решения единствено за определени стойности на енергията, наречени характерни стойности.

За водородния атом, характерните стойности на енергията са дадени чрез зависимостта: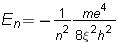

където:  m и  e са масата и заряда на електрона

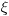 : диелектричната проницаемост на вакуум

                         h : константата на Планк

n  е число, което може да заема стойности 1, 2, 3, и т.н. Това число се идентифицира с главното квантово число, присъстващо в модела на Бор. В математическото определяне на вълновата функция се получават и другите две квантови числа  l и m.

Уравнението на Шрьодингер не може да бъде решено освен за системи с един единствен електрон: водород и водородоподобни йони като He+ или Li2+ . Когато има повече електрони ситуацията е много  по-комплексна тъй като освен взаимодействието ядро-електрон (привличане с ядрото), се появяват взаимодействия електрон – електрони (ефекти на отблъскване между електроните) които зависят от позициите на двете частици:

Решенията на уравнението на Шрьодингер, независими от времето, са квантовите състояния, описващи едновременно електроните. Те са описани математически от една  “многоелектронна” вълнова функция, зависеща от пространствените координати и от спина на  Z електрона. След опростявания тя се отбелязва като се взима предвид само броя на електроните:

 (1, 2, ..., З)

Няма познато аналитично решение на съответното уравнение на Шрьодингер. Търсят се близки решения, които не са само математически, но съдържащи в себе си  разглежданите концепции и са приложими независимо от разглеждания атом.