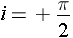|
Influence de l'angle i sur la déviation.
|
|
|
 Considérons le montage expérimental ci-contre: il se compose d'un plateau tournant, gradué, sur lequel est disposé un prisme d'angle A et d'indice n, dont on a pris soin de placer la face d'entrée perpendiculairement au repère 0-180° et l'arête sur l'axe de rotation du disque. Une source lumineuse S fournit un pinceau de lumière monochromatique dont la largeur est juste suffisante pour qu'au voisinage de A, l'arête du prisme coupe le pinceau en deux parties: l'une ,qui passe au dessus du prisme, vient frapper en O l'écran d'observation E; l'autre en revanche le traverse et subit une déviation suivant AF. L'animation suivante illustre l'existence d'un minimum de déviation pour le prisme: A l'aide de ce dispositif qui permet d'atteindre facilement la valeur des angles i et D, cherchons à construire la courbe qui lie ces deux grandeurs. Commençons pour cela par nous placer en incidence rasante:
le pinceau émergent vient alors frapper l'écran en Fo, ce qui correspond à une déviation maximale Do. Tournons maintenant progressivement le disque gradué, dans le sens trigonométrique: l'angle d'incidence i diminue et sur l'écran le point F se rapproche de O jusqu'à une position Fm dont il s'éloigne ensuite pour retrouver lorsque i atteint une certaine valeur io, sa position de départ en Fo. Au niveau de l'angle D dont les variations suivent celles de la longueur OF, il en résulte que la déviation passe donc par un minimum Dm pour une valeur im de l'angle d'incidence, avant de reprendre sa valeur de départ Do lorsque i = io, c'est-à-dire lorsqu'il y a émergence rasante du pinceau lumineux.  Lorsqu'un pinceau lumineux traverse un prisme, il subit une déviation D qui dépend de son angle d'incidence i; en particulier, il existe une valeur im de i pour laquelle l'angle de déviation est minimal. |