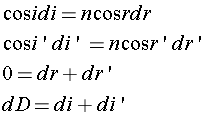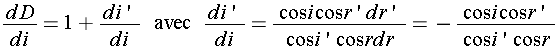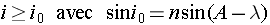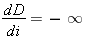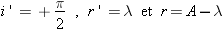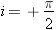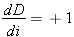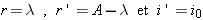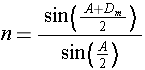|
Déviation D en fonction de l'angle d'incidence i.
|
|
||||||||
|
Considérons la fonction f qui par l'intermédiaire des formules du prisme lie D à A, n et i. Différentions ces relations, en laissant constant A et n:
De ce système il est possible d'extraire l'expression de la dérivée de dD/di:
ce qui entraîne: 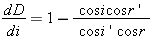 Pour déterminer le signe de cette dérivée et en déduire le sens dans lequel la déviation évolue en fonction de l'angle d'incidence, recherchons le domaine de variation de i. Celui-ci est pour une part imposé par les conditions d'émergence du prisme qui nous précisent notamment que:
De plus: 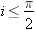 . Calculons la valeur de dD/di aux bornes de l'intervalle: . Calculons la valeur de dD/di aux bornes de l'intervalle: 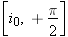
On voit aussi que la dérivée change au moins une fois de signe entre io et 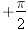 . .cherchons les valeurs de di pour lesquelles dD/di = 0. Celles ci sont les racines de l'équation: 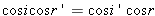 ou encore de ou encore de 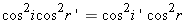 Compte tenu des formules de Descartes, cette relation peut être transformée; elle conduit après simplification, à l'équation: 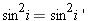 dont les racines sont: dont les racines sont: 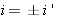 La solution i = - i' n'est pas recevable physiquement car elle entraîne r = - r' c'est-à-dire A = 0. Il n'existe donc qu'une seule valeur de i pour laquelle dD/di = 0; cela signifie que la déviation D ne présente qu'un seul extremum. Comme le montre le tableau de variation de la fonction: celui-ci est un minimum qui correspond à D = Dm avec: Dm = 2 im - A si im désigne la valeur commune aux angles i et i'. Remarquons par ailleurs qu'aux bornes de l'intervalle de variation de i, la déviation est maximale et égale à: 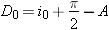 En dehors de ces résultats qui confirment bien ceux obtenus expérimentalement, l'étude théorique de la fonction D = f(i) fournit des informations complémentaires intéressantes. Ainsi on note que la fonction est continue entre io et 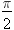 ; il en résulte qu'à une même valeur D de la déviation , il ne peut correspondre sur la courbe que deux points P et Q d'abscisses respectives i et i'. Cela signifie au niveau de la marche des rayons lumineux à travers le prisme, qu'il n'existe que deux valeurs de l'angle d'incidence, et deux seulement, pour laquelle la lumière est déviée de la même amplitude; ; il en résulte qu'à une même valeur D de la déviation , il ne peut correspondre sur la courbe que deux points P et Q d'abscisses respectives i et i'. Cela signifie au niveau de la marche des rayons lumineux à travers le prisme, qu'il n'existe que deux valeurs de l'angle d'incidence, et deux seulement, pour laquelle la lumière est déviée de la même amplitude;En dehors de ces résultats qui confirment bien ceux obtenus expérimentalement, l'étude théorique de la fonction D = f(i) fournit des informations complémentaires intéressantes. Ainsi on note que la fonction est continue entre io et 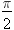 ; il en résulte qu'à une même valeur D de la déviation , il ne peut correspondre sur la courbe que deux points P et Q d'abscisses respectives i et i'. Cela signifie au niveau de la marche des rayons lumineux à travers le prisme, qu'il n'existe que deux valeurs de l'angle d'incidence, et deux seulement, pour laquelle la lumière est déviée de la même amplitude; ; il en résulte qu'à une même valeur D de la déviation , il ne peut correspondre sur la courbe que deux points P et Q d'abscisses respectives i et i'. Cela signifie au niveau de la marche des rayons lumineux à travers le prisme, qu'il n'existe que deux valeurs de l'angle d'incidence, et deux seulement, pour laquelle la lumière est déviée de la même amplitude;si I et I' sont les angles d'émergence correspondants respectivement à ces angles d'incidence i et i' ,on a donc: i + I - A = i' + I' - A , compte tenu de l'expression générale de la déviation. Or cette égalité doit être compatible avec le principe de retour inverse de la lumière; pour qu'il en soit ainsi, la seule solution possible est que: I = i' et I' = i. Autrement dit, sur la courbe D = f(i) , deux points P et Q d'abscisses respectives i et i' ne peuvent avoir la même ordonnée, c'est à dire la même déviation, que si celle-ci a pour valeur: D = i + i' - A Il est intéressant de remarquer que cette expression de D peut être transformée pour faire apparaître les coordonnées 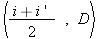 du point H milieu du segment PQ. EN effet exprimée sous la forme: du point H milieu du segment PQ. EN effet exprimée sous la forme: 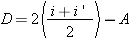 cette relation n'est autre que l'équation de la droite suivant laquelle se répartissent les points milieux des cordes telles que PQ, lorsque D varie de Do à Dm. Cette droite de pente +2 et dont l'ordonnée à l'origine a pour valeur -A , coupe évidemment la courbe D = f ( i ) en son minimum de déviation. Cette propriété est souvent mise à profit pour déterminer Dm. En effet, pour connaître avec précision la valeur minimale de la déviation, à partir de la courbe expérimentale D = f ( i ) d'un prisme, il suffit de relever l'ordonnée du point d'intersection de cette courbe avec la droite: cette relation n'est autre que l'équation de la droite suivant laquelle se répartissent les points milieux des cordes telles que PQ, lorsque D varie de Do à Dm. Cette droite de pente +2 et dont l'ordonnée à l'origine a pour valeur -A , coupe évidemment la courbe D = f ( i ) en son minimum de déviation. Cette propriété est souvent mise à profit pour déterminer Dm. En effet, pour connaître avec précision la valeur minimale de la déviation, à partir de la courbe expérimentale D = f ( i ) d'un prisme, il suffit de relever l'ordonnée du point d'intersection de cette courbe avec la droite: 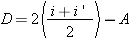 qui peut être construite expérimentalement ,soit en traçant le lieu géométrique des points milieux des cordes parallèles à l'axe des abscisses i du graphe D = f ( i ), soit en déterminant par une mesure indépendante la valeur de l'angle A du prisme. qui peut être construite expérimentalement ,soit en traçant le lieu géométrique des points milieux des cordes parallèles à l'axe des abscisses i du graphe D = f ( i ), soit en déterminant par une mesure indépendante la valeur de l'angle A du prisme.Il est une autre remarque qui mérite d'être faite à propos du minimum de déviation. Nous avons vu en effet que pour D = Dm, i = i' = im ; ceci entraîne que r = r' = rm =A/2 . Autrement dit : lorsqu'un rayon lumineux traverse un prisme au minimum de déviation, son trajet est symétrique par rapport à la bissectrice de l'angle A du prisme. Par ailleurs puisque Dm = 2 im - A, on a 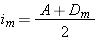 La loi des sinus de Descartes s'exprime donc au minimum de déviation sous la forme: 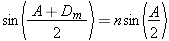 d'où l'on peut tirer: d'où l'on peut tirer:
Cette relation est importante, car elle est à la base de la mesure des indices de réfraction par la méthode dite du minimum de déviation du prisme. Celle-ci, qui consiste à rechercher expérimentalement la valeur de A et celle de la déviation Dm subie par un rayon lumineux monochromatique, permet d'atteindre n avec 5 décimales exactes. La méthode est applicable aux solides, mais également aux liquides; dans ce dernier cas, on utilise un prisme creux dans lequel on verse le liquide à étudier. |